Sensual Mathematics

Mathematical Garden that plays with Platonic solids

DESIGN OVERVIEW

What is more sensual than a garden in full bloom? From our starting point knowing only the name of the exhibition in Heureka, Sensual Mathematics, we started grabbing for mathematical imagery to express sensuality with art. These figures were then brought together and narrowed down to a concept idea to express both a scientific abstraction as well as express beauty and awe. Further work produced sketches of an installation with three dimensional solids to form a mathematical garden. Holding true to our idea we present to you the Mathematical Garden.

MATHEMATICAL SPECIFICATIONS

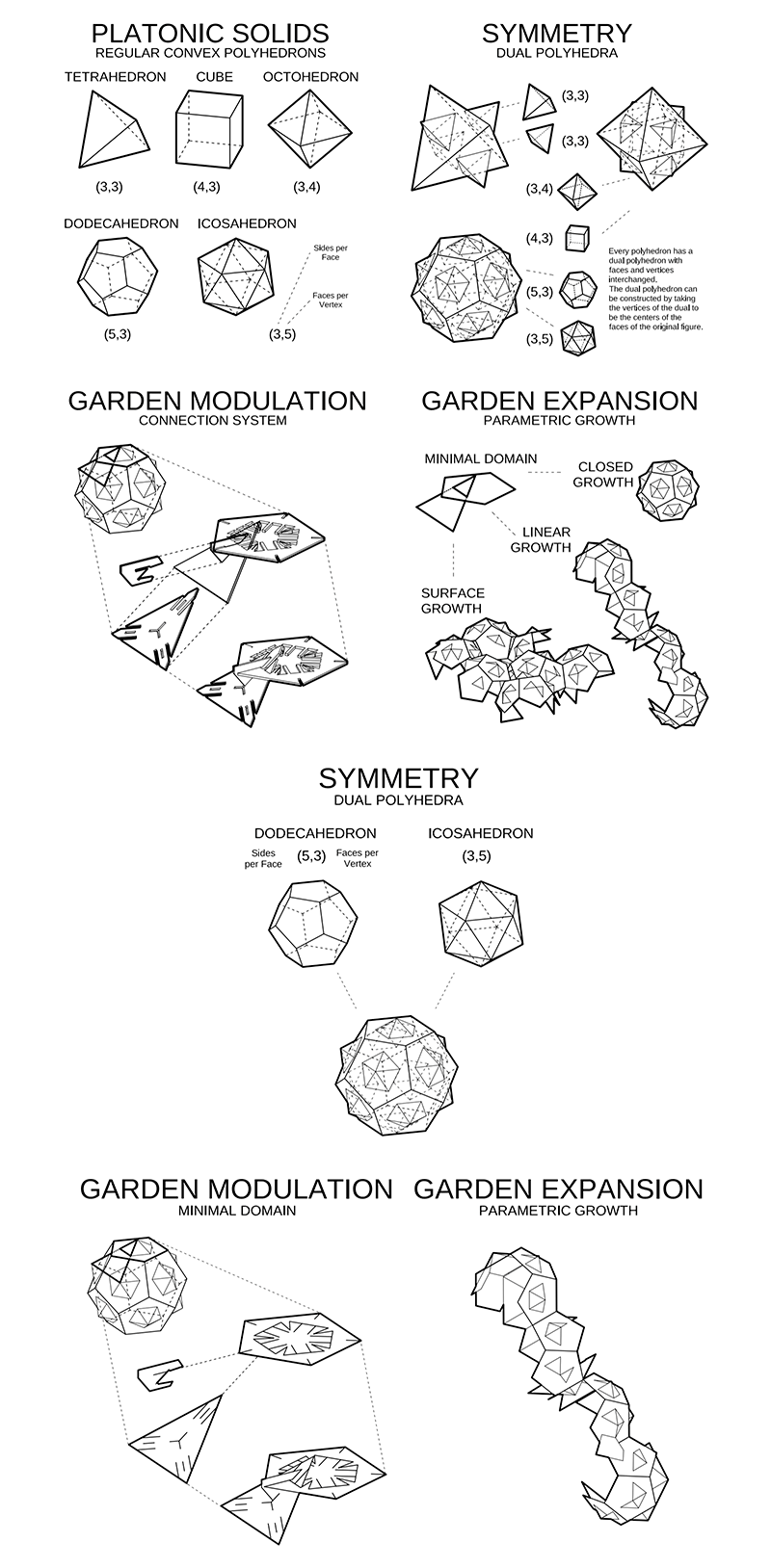
We started our journey to the Mathematical Garden with the five Platonic solids, named after the ancient Greek philosopher Plato who described them in one of his dialogues, Timaeus (53a-55d) ca. 360 B.C. Plato thought that these five regular and convex polyhedrons, namely tetrahedron, cube, octahedron, dodecahedron and icosahedron were the most beautiful solids on the Earth and, in fact, correspond the four basic elements and the whole cosmos.

From these five solids we chose two different solids to play with: dodecahedron, consisting of 12 pentagonal faces, and icosahedron which consists of 20 triangular faces. At first glance these two solids appear quite different from each other. However, they are related in many ways, especially because they are duals of each other. That is, for each pentagonal face of a dodecahedron, there is a vertex of an icosahedron where five triangular faces meet. Of course, this goes also vice versa: for every vertex of a dodecahedron where three pentagonal faces meet, there is corresponding face of the icosahedron. In other words, one can pair all the faces of one solid with the vertices of the other solid.

If you look closely at the ball-like solids in the garden you can see that there is a dodecahedron and a tetrahedron overlapping so that in the each face of one solid there is exactly one vertex of the other solid overlapping.

Finally one can count all the vertices and faces and end up with these numbers:

• Dodecahedron: 12 faces - 20 vertices - 3 meeting edges per vertex - 5 edges per face
• Icosahedron: 20 faces - 12 vertices - 5 meeting edges per vertex - 3 edges per face

Now you can easily see how these two solids are related to each other! Similar relations apply among the other Platonic solids: cube and octahedron are duals of each other and, tetrahedron is a dual of itself.

In the Mathematical Garden one can find some icosahedrons and dodecahedrons and then see how their triangular and pentagonal building blocks abandon the original Platonic shape and start to grow in variety of directions and forms.

GROUP: Think-a-Ton

Julia Isotalo
School of Science, Information Networks (SCI), julia.isotalo@aalto.fi, https://fi.linkedin.com/in/julia-isotalo-875322137

Laura Meskanen-Kundu
School of Arts, New Media Design and Production (ARTS), laura.meskanen-kundu@aalto.fi, www.lauramk.me, https://fi.linkedin.com/in/laura-meskanen-kundu-CV

Parvati Pillai
School of Art, Visual Communication Design (ARTS), parvati.pillai@aalto.fi, https://www.behance.net/parvati

Pedro Pablo Garcia Alcazar
School of Arts, Design and Architecture (ARTS), pedro.garciaalcazar@aalto.fi, https://es.linkedin.com/in/pedro-pablo-garcia-alcazar-94577489

Ville Romanov
School of Science, Mathematics (SCI), ville.romanov@aalto.fi, http://www.linkedin.com/in/ville-romanov-363a2a8a

More from here & from google drive

Otaniemi Stories can be found here & our work was seen in MeNaiset